 |
| God's Equation |
The Derivation of E=mc2
Perhaps the most famous
equation of all time is E = mc2. The equation is a
direct result of the theory of special relativity, but what does
it mean and how did Einstein find it? In short, the equation
describes how energy and mass are related. Einstein used a brilliant thought experiment to
arrive at this equation, which we will briefly review here.
First of all, let us consider a particle of
light, also known as a photon. One of the interesting properties of photons is
that they have momentum and yet have no mass. This was established in the
1850s by James Clerk Maxwell. However, if we recall our basic physics, we know
that momentum is made up of two components: mass and velocity. How can a photon
have momentum and yet not have a mass? Einstein’s great insight was that the
energy of a photon must be equivalent to a quantity of mass



Einstein’s thought experiment runs as
follows. First,
imagine a stationary box floating in deep space. Inside the box, a
photon is
emitted and travels from the left towards the right. Since the
momentum of the
system must be conserved, the box must recoils to the left as the
photon is
emitted. At some later time, the photon collides with the other
side of the
box, transferring all of its momentum to the box. The total
momentum of the
system is conserved, so the impact causes the box to stop moving.
Unfortunately, there is a problem. Since no
external forces
are acting on this system, the centre of mass must stay in the
same location.
However, the box has moved. How can the movement of the box be
reconciled with
the centre of mass of the system remaining fixed?
Einstein resolved this apparent contradiction
by proposing
that there must be a ‘mass equivalent’ to the energy of the
photon. In other
words, the energy of the photon must be equivalent to a mass
moving from left
to right in the box. Furthermore, the mass must be large enough so
that the
system centre of mass remains stationary.
Let us try and think about this experiment
mathematically.
For the momentum of our photon, we will use Maxwell’s expression
for the
momentum of an electromagnetic wave having a given energy. If the
energy of the
photon is E and the speed of light is
c, then the momentum of the photon is
given by:
(1.1)
The box, of mass M,
will recoil slowly in the opposite direction to the photon with
speed v. The momentum of the box is:
(1.2)
The photon will take a short time, Δt,
to
reach the other side of the box. In this time, the box will have
moved a small
distance, Δx. The
speed of the box is therefore given by
(1.3)
(1.4)
If the box is of length L,
then the time it takes for the photon to reach the other side of
the box is
given by:
(1.5)
Substituting into the conservation of momentum
equation (1.4)
and rearranging:
(1.6)
Now suppose for the time being that the
photon has some
mass, which we denote by m. In this
case the centre of mass of the whole system can be calculated.
If the box has
position x1 and the photon
has position x2, then the centre of mass for the whole
system is:
(1.7)
We require that the centre of mass of the whole
system does
not change. Therefore, the centre of mass at the start of the
experiment must
be the same as the end of the experiment. Mathematically:
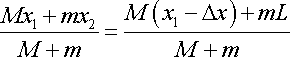
(1.8)
The photon starts at the left of the box, i.e.
x2 = 0. So, by rearranging and
simplifying the above equation, we get:
Substituting (1.4)
into (1.9)
gives:
(1.10)
Rearranging gives the final equation:
So, let’s think about what this equation means. The equation suggests that a given mass can be converted into energy. But how much energy? Well, suppose we have a kilo of mass. Conversion of this mass into pure energy would result in (1kg * c2) joules of energy. Now note that c2 = 8.99 * 1016 m2s-2
In practice, it is not possible to convert all
of the mass
into energy. However, this equation led
directly to the development of nuclear energy and the nuclear bomb
- probably the most tangible results of special relativity.